相加平均と相乗平均の大小関係を円の半径から考える
注) 本記事は数学に関するものであり、バイオインフォマティクスとは関係ありません。前回までの記事で行っていた解析の続きを読みたい方は、次回の更新をお待ちください。
私の趣味の一つが数学なので、今後は数学に関する面白いと思ったお話などを書いてみようと思います。
今回は、高校数学で学習する「相加平均・相乗平均の大小関係」に関するお話です。
相加平均・相乗平均の定義と性質
(本記事では、0以上の2つの数の平均について考えることにします。)
簡単に言えば、相加平均は2つの数の和を2で割ったもので、相乗平均は2つの数の積の負ではない平方根です。
数式で定義すると、以下のようになります。
2つの実数 \( x \ge 0, y \ge 0 \) に対して、
相加平均: \[ \frac{x + y}{2} \]相乗平均: \[ \sqrt{xy} \]また、相加平均と相乗平均には、以下の性質があります。
\[ 相加平均 \ge 相乗平均 \]\( x = y \) の時のみ、\[ 相加平均 = 相乗平均 \]今回はこの性質を、円を使って視覚的に証明してみます。
証明
最初に、\( x = 0 \) or \( y = 0 \) の場合、相乗平均が 0 になるため、上記の性質は明らかに成り立ちます。
そのため、証明では \( x > 0 \) and \( y > 0 \) の場合を考えることにします。
証明には、方べきの定理を利用します。方べきの定理とは、円と円周上以外のどこかにある点について、点から円に交わるように線を引くと、点から2つの交点までの距離の積が常に一定になるというものです (線が円に接するように引いた場合は、点から接点の距離の2乗を考えることができます)。
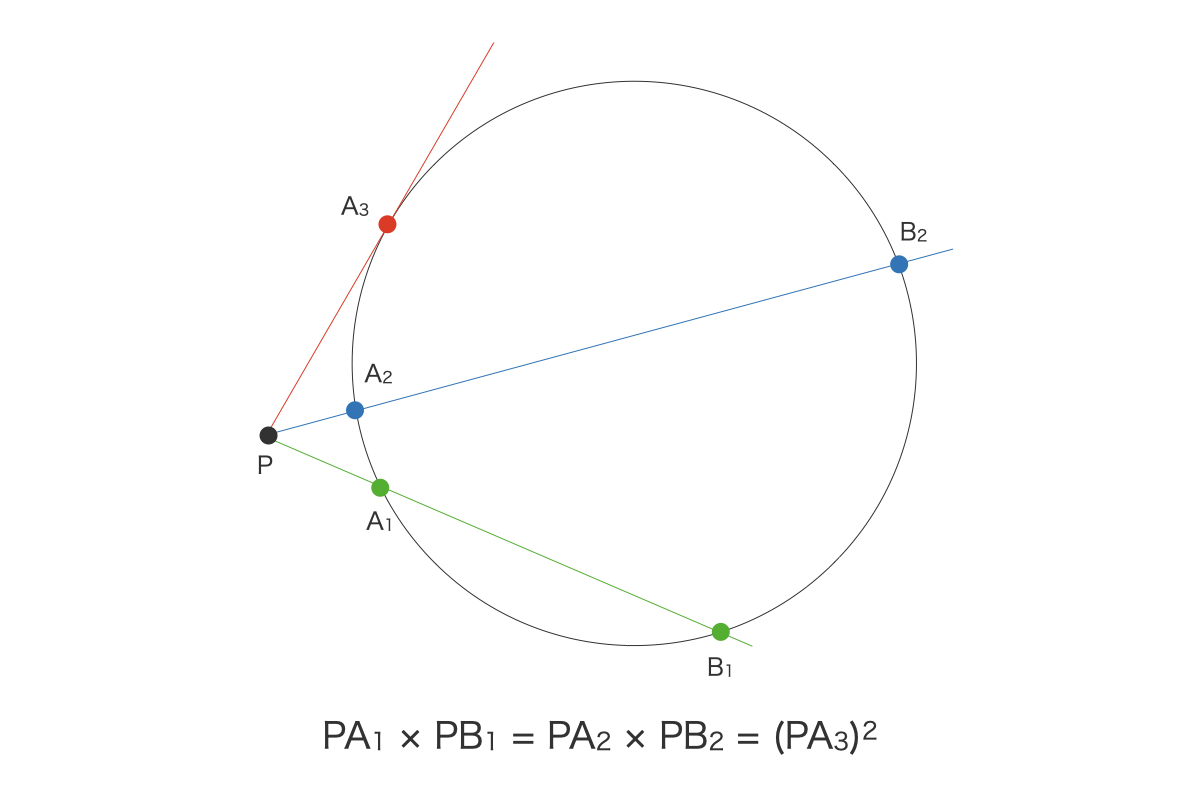
方べきの定理の証明については、Wikipedia などをご参照ください。この定理を利用して、円の半径、および直径から相加平均、相乗平均を計算し、その大小関係を視覚的に捉える方法を考えます。
最初に、円と直径を用意して、その交点を A, B とします。円の中心を O として、線分 AB に垂直な半径を引き、円との交点を C とします。
次に、線分 AB 上の、A, B, O ではないところに、自由に点 P をとり、AB と垂直な線を引き、円との交点をそれぞれ D, E とします。
この時、方べきの定理により、\( PA \times PB = PD \times PE \) が成り立ちます。
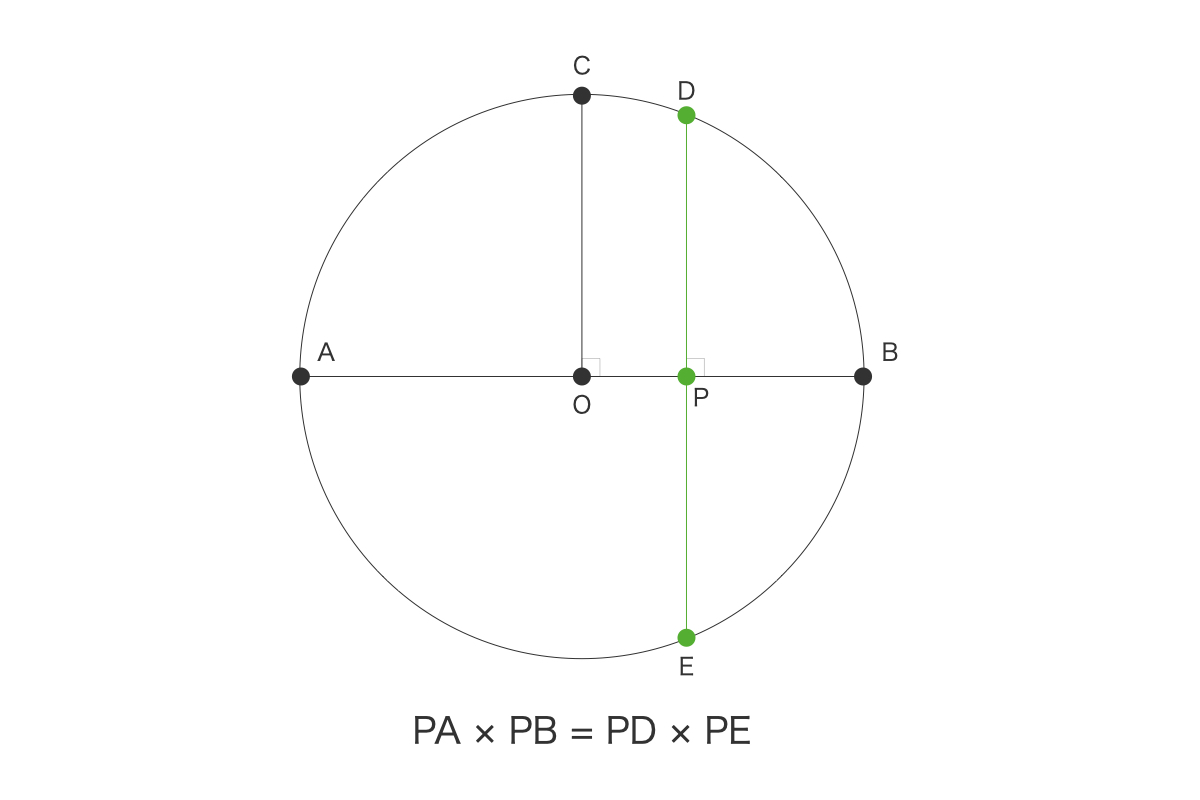
図形の対称性から、明らかに \( PD = PE \) なので、\( PA \times PB = PD^2 \) が成り立ちます。
ここで、\( PA = x, PB = y \) とすると、\( PA + PB = 直径 \) であることから、\[ \frac{x + y}{2} = 半径 \]すなわち、\[ 相加平均 = 半径 \]であることがわかります。
また、\( PA \times PB = PD^2 \) から、\[ x \times y = PD^2 \]両辺は正の数なので、正の平方根を取ると、\[ \sqrt{xy} = PD \]すなわち、\[ 相乗平均 = PD \]であることがわかります。
PD は点 P の位置によって、半円の中を直径 AB と垂直になるように動くので、半径よりも大きくなることはありません。そのため、相加平均が相乗平均よりも小さくなることはないことが、視覚的にわかります。
また、点 P が円の中心 O と重なる時にのみ、\(PD = 半径\) であることから、等号が成立する条件が \( PA = PB \)、すなわち \(x = y\) であることもわかります。
今回は以上です。